티스토리 뷰
최단 경로 알고리즘
주어진 노드(node)와 간선(edge)들 중, 가장 짧은 경로를 찾는 알고리즘이다.
최단 경로 문제는 아래와 같이 3가지로 주어질 수 있다.
1. 특정 노드에서 시작해 특정 노드까지 도착하는 가장 짧은 경로
2. 특정 노드에서 시작해 모든 노드까지 도착할 수 있는 가장 짧은 경로
- 이동 경로 양수 시, Dijkstra 알고리즘
- 이동 경로 음수 포함 시, Bellman-ford 알고리즘
3. 모든 노드에서 시작해 모든 노드까지 도착할 수 있는 가장 짧은 경로 (Floyd Warshall 알고리즘)
다익스트라 알고리즘 (Dijkstra Algorithm)
다익스트라 알고리즘은 특정 노드에서 시작해 인접한 노드의 가장 짧은 경로들을 탐색하며 모든 노드의 최소 경로를 구하는 알고리즘이다.
Greedy 알고리즘으로, 현재 상황에서 최선의 선택을 진행하며 단방향, 양방향 모두 사용할 수 있다.
[알고리즘 흐름]
1. 출발 노드 설정
2. 최단 거리 테이블을 무한대로 초기화
3. 방문 체크 테이블을 모두 false로 초기화
4. 출발 노드는 방문했다고 true 체크
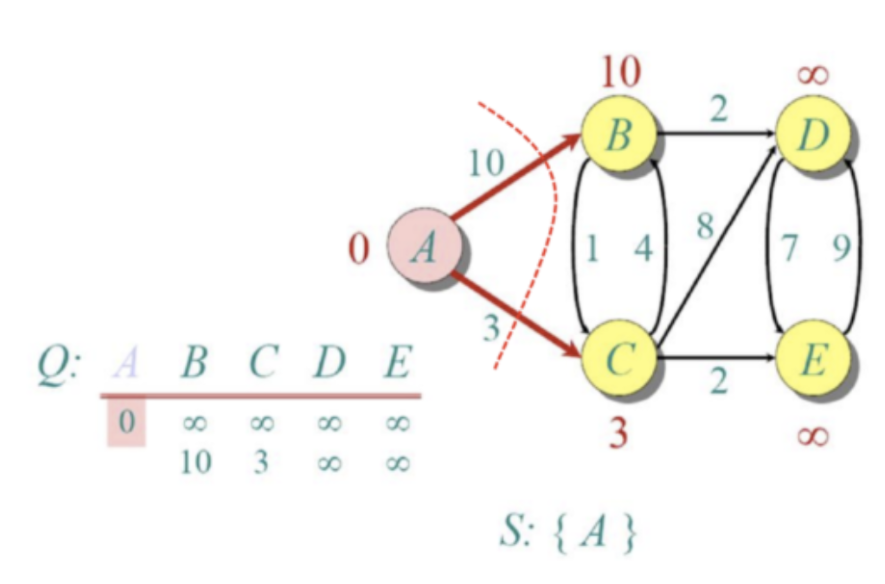
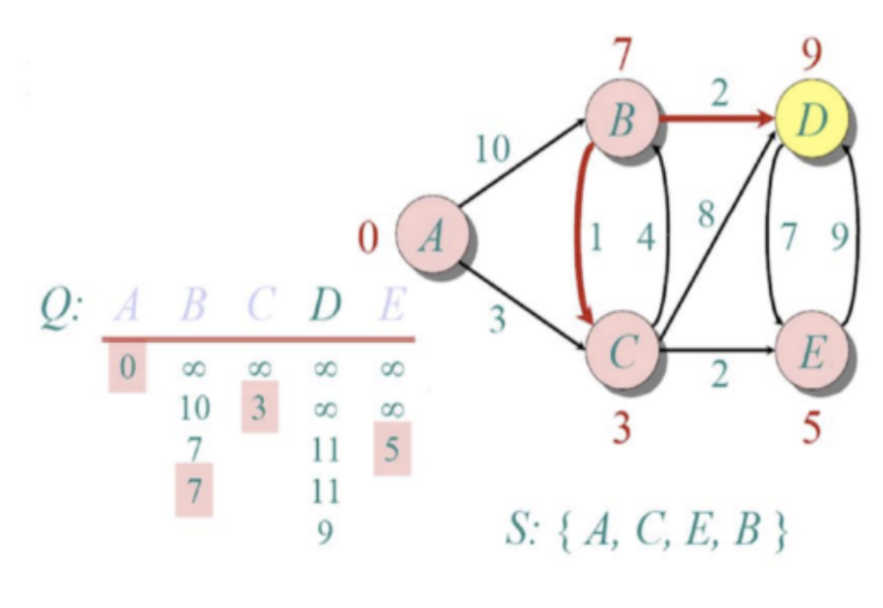
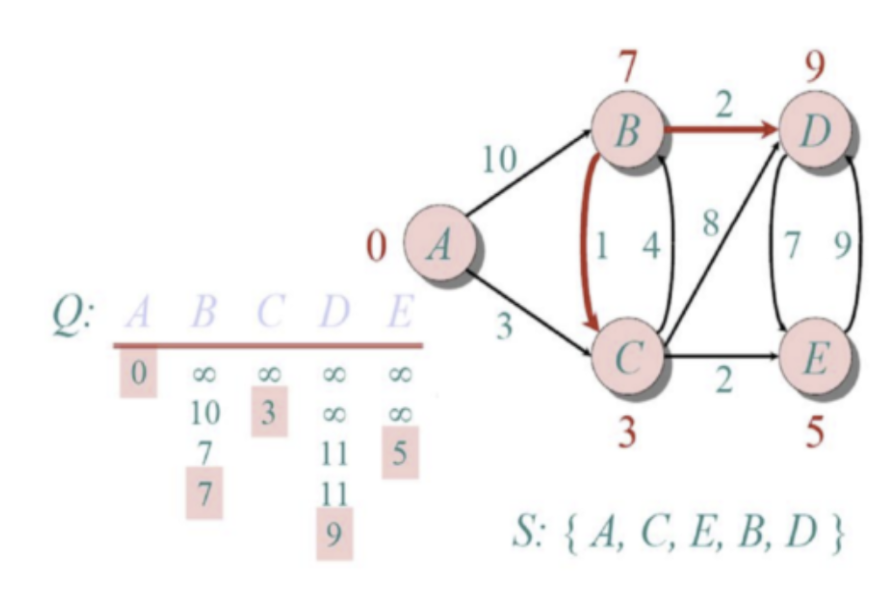
5. 출발 노드로부터 연결되어있는 노드들의 거리를 비교해 최단거리 테이블 갱신
6. 아직 방문하지 않은 노드 중, 최단 거리 테이블의 값이 가장 작은 노드를 선택
7. min (방금 선택한 노드의 최단거리 테이블 값 + 앞으로 갈 노드 x까지의 값, 현재 최단거리 테이블의 x 값) 으로 최단거리 테이블 갱신
(5~6 반복)
위의 알고리즘 구현 시, 매번 선형 탐색 해야하므로 시간복잡도가 N^2이 걸린다.
따라서 logN의 시간복잡도를 갖는 우선순위 큐를 사용할 수 있다.




시간복잡도
주어진 노드 간의 모든 간선을 이동하며 검사하므로 간선의 개수만큼의 시간이 소요된다. O(E)
데이터에 대한 삽입/삭제가 최악의 경우에 간선에 개수만큼 발생하므로 O(E)이고 삽입/삭제가 발생했을 때, 최소 힙을 유지하는 비용은 O(logE)가 발생한다. O(ElogE)
즉, O(E) + O(ElogE) = O(ElogE)
코드
import heapq
import sys
input = sys.stdin.readline()
INF = int(1e9) #무한을 의미하는 값으로 10억을 설정.
#노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
#시작 노드 번호를 입력받기
start = int(input())
#각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
#최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)
#모든 간선 정보를 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
#a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b, c))
def dijkstra(start):
q = []
#시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
heapq.heappush(q, (0, start))
distance[start] = 0
while q: #큐가 비어있지 않다면
#가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if distance[now] < dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:
cost = dist + i[1]
#현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
dijkstra(start)
#모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n + 1):
#도달할 수 없는 경우, 무한이라고 출력
if distance[i] == INF:
print("INFINITY")
#도달할 수 있는 경우 거리를 출력
else:
print(distance[i])'Coding - Algo > 알고리즘&자료구조' 카테고리의 다른 글
| 최소 신장 트리(MST) - 크루스칼 알고리즘 / 프림 알고리즘 (0) | 2021.08.25 |
|---|---|
| 최장 증가 부분 수열(LIS) 알고리즘 (0) | 2021.04.04 |
| 유니온 파인드(UNION-FIND) 파이썬 / 자바 구현 (0) | 2021.03.31 |
- Total
- Today
- Yesterday
- 프로그래머스 파이썬
- 프로그래머스
- 삼성청년SW아카데미
- yoloV3
- swea 타일링
- 1240 자바
- swea 4070 타일링
- 타일링 자바
- 메뉴리뉴얼 풀이
- 백준 풀이
- 우분투
- 파이썬
- swea 1240 자바
- SSAFY
- 1699 자바
- 백준 17144
- 백준파이썬
- 프로그래머스 더 맵게
- poker swea
- 파이썬 풀이
- swea 1240
- ubuntu
- 더 맵게
- 3996 자바
- 백준 dp 문제
- swea 타일링 자바
- 백준
- 프로그래머스 자바
- SWEA
- union-find
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
